|
今天看了一篇访谈《章文嵩、蒋晓伟、李飞飞、张凯巅峰对谈:大模型时代的数据智能新趋势》[1], 其中飞刀老师谈到一些多模态数据库的内容,恰好昨天看到丘成桐老先生的视频讲“人工智能没有办法产生观念上的突破” 数学的发展,每走一步是观念上的发展和观念的改变,对数学发生了翻天覆地的变化。
当然对于AI是否能够产生新的数学观念, 我不清楚. 但人工智能大模型演进到多模态时,所有的App基础设施对于数据的观念是否也会像数学本身那样带来翻天覆地的变化呢? 答案是显然的.正如我在很多年前一直在谈的和最近在《大模型时代的数学基础》这个系列文章中阐述的:
这一次人工智能革命的数学基础是:范畴论/代数拓扑/代数几何这些二十世纪的数学第一登上商用计算的舞台。
传统的数据库基于集合论和关系, 并通过集合论的视角进行运算, 例如查询:选择、投影、连接、除、并、交、差, 数据更新:插入、删除、修改. 另一方面现代的面对对象编程本身也是受集合论观点的影响. 而集合论观点出发的关系是二元的, 要么真要么假. 因此无论是面对对象编程还是数据库, 但关系一直处在变化的过程中,大家可能更需要的是知道某个属性在什么时候为真, 因此解决一致性问题成为当今分布式系统的最核心的问题。
但是,是否有另一种数学的观念存在呢? 大家想象一下罗素悖论,更通俗的描述是:“一个城市里唯一的理发师立下了以下的规定:只帮那些自己不理发的人理发。” 正好前天成了罗素悖论的践行者, 自己给自己理发这事情如何定义呢? 拥抱变化才是出路。
另一方面,大家注意到对于Transformer模型在多模态下的说明, ilya点赞了一篇柏拉图表征假说的论文:
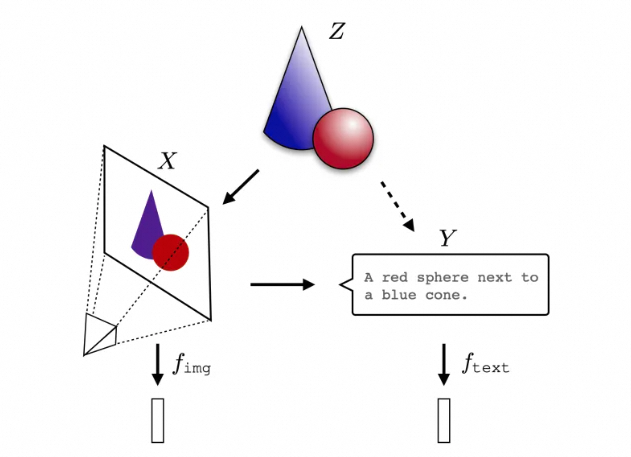
本质上这些内容在数学上早就有了定义, 那就是TOPOS理论. 大家先来谈谈范畴论
阿蒂亚将数学描述为“类比的科学”。在这一领域,范畴论的视野是数学的类比。范畴论提供了一种跨学科的数学语言,旨在勾勒出一般现象,这使得思想可以从一个研究领域转移到另一个领域。范畴论的观点可以作为一个简化的抽象概念,它将那些出于形式原因成立的命题与那些需要特定数学学科的技术来证明的命题隔离开。微妙的视角转变使得数学内容可以用一种对考虑的对象种类相对漠不关心的语言来描述。范畴论的方法不是直接对对象进行刻画,而是强调同一通用类型的对象之间的变换。
范畴论是数学的一个跨学科的领域,它采用了一种新的视角来理解数学现象。与数学的大多数其他分支不同,范畴论对被考虑的对象本身不太感兴趣。相反,它专注于同一类型对象之间以及不同类型对象之间的关系。它的抽象性和广泛性使它能够触及并连接数学的几个不同分支:代数、几何、拓扑、分析等。
而当大家以范畴论的视角来看待《Attention is all you needs》时, 你会恍然大悟:不就是一个态射么? 那么反过来,大家如何定义一个对象? 当然有Java/C++这些OOP的class的定义方式, 是否存在另一种方式呢? 像Golang这样的Struct with Function/Method呢?
其实范畴论的米田引理(Yoneda Lemma)就在讲这个事情,简单来说:“人的本质是一切社会关系的总和”, 也就是说一个对象, 其实大家可以通过指向它的箭头(以范畴论的视角为态射, 以AI的视角为Attention)的方式来刻画. 这也是我在《大模型时代的数学基础(2)》中讲到的:
对于一个对象A,大模型的预训练过程实际上是通过尽量多的数据来构建A和其它对象的Attention的集合,实际上是,它是一个反变函子,也可记为定义 函子范畴中最重要的一个例子就是预层(presheaf)范畴,记为, Presheaf是C上的一个函子, 上的所有presheaf构成的对象和presheaves之间的自然变换构成态射,这样的范畴被成为预层范畴。本质上大模型的预训练过程实际上就是需要构造一个预层范畴。
然后大家就可以引入TOPOS的概念了, 在此之前还说一句, 有些人总是说HUAWEI搞的数学都不是数学. 但我知道的是2002年菲尔兹奖得主 Laurent Lafforgue在2021年加入了HUAWEI, 参与Topos理论的发展与其潜在应用

黄大年茶思屋还有一个很好的专题《Lagrange AI Math Cornerstone Course》[2] 大约在1963年, Bill Lawvere决定根据范畴论找出一种新的数学基础。他的想法是从严格的范畴论角度出发来构造集合论的概念。范畴论是一个更加一般化的结构理论,利用对象之间的态射来描述结构的性质,而不是像集合论那样通过元素(elements)和成员关系(membership)来描述。因此,“集合”或“空间”的集合论概念被“对象”取代,而“元素”被“箭头”或“态射”取代。从范畴论的视角来分析集合论淡化了membership而强调了函数性
1966年春天,Lawvere遇到了Grothendieck在代数几何中发明的“Topos”概念。Topos在希腊语中的意思是“Place”,在代数几何中,大家常常不仅对某个事物是否为真感兴趣,而对它在哪里为真感兴趣,例如给定空间中的两个函数,它们在哪相等?
Grothendieck对此进行了认真思考斌发明了他的Topos概念,大概来讲它是一个可以充当为一个进行数学研究的“place”的范畴(a category that serves as a place in which one can do mathematics)。最终,这导致了一种真理的概念,其中内含了非常广泛意义上的“空间”概念!
到了1971年,Lawvere和Myles Tierney对Grothendieck最初的Topos概念(现在被称为Grothendieck Topos) 进行了概括和提炼,并提出了“Elementary Topos”的概念。
Topos是具有额外的某些属性的范畴,使其很像集合范畴。有很多不同的Topos,你可以在所有的这些Topos中做相同的运算,但同时它们之间也存在很多差异,例如选择公理不必在Topos中成立,排中律()也不需要成立。原因是真理并不是一个 yes-or-no的问题,相反大家需要最终如何为真的陈述,或者更准确的说,在哪为真。那么在这样的视角下, 大家是否能够去重新构造大家的App基础设施和算法呢?正好最近还看到一篇论文《Benchmarking Benchmark Leakage in Large Language Models》[3],花了那么多算力提高的Benchmark能够应对变化么? 大家是特别擅长应付各种考试, 把训练搞成了应试教育, 却少了从根本上改变观念创新的勇气(此处要给DeepSeek团队点一个的赞, 无论是MLA还是Shared Expert 的MoE, 以及以上的那篇论文的结果,这个团队的都是在国内顶尖的.)
对于多模态的成功,或许大家应该去进一步读一本书
对比集合论和范畴论概念之间的基本对应关系如下:
而这些数学观念上的变化,正是大模型时代的数据智能所需要的. 大家是否还需要用像素和坐标系来刻画一张图片? 是否能用TOPOS理论中的Subobject Classifier来说明MoE模型?
在推理过程中的Speculative Decoding和传统标量处理器的Branch Prediction本质上是否是相通的Latency Hidding过程? 是否都能通过Subobject Classifier来说明? 基于范畴论视角下的多模态数据库建模是否可以显著的提高性能?并取代基于关系代数构建的数据库?
例如将Vocab进一步扩大构建更大的态射, 对于空间数据的重新建模, 对于Mel-Spectrum的语音数据建模, 然后在一个统一的可表空间构造态射, 似乎又多了几分函数式编程的味道。
这些问题都是大家值得去深思的, 都是一些能够进入教科书的工作, 这才是能够从根本上去解决大模型的算法的路径,而不是一个简单的Scalling Law或者data compression的视角. 可惜搞纯数的人看不上觉得low, 搞CS的人又很多不懂数学,甚至是不懂得敬畏数学。
举个小例子, 推理的时候, 延迟不满足要求,中间用一些小模型穿插一些语气词来模拟人真实的思考过程, 例如: ”嗯~~,让我想想...大概是这样的” , 而对于模型对齐和安全的问题, 也有很多巧妙的做法。
算力不够, 多一分豁达. 名利面前, 多一分宽容. 算法面前, 多一份谦卑. 正如弘一法师所讲
转自:zartbot
| 
 303
303
 303
303